UberのMarketing Mix Modeling論文を読んでみた所感

はじめに

初めまして、データ戦略室データサイエンスグループの徳田です。以前のブログでMarketing Mix Modeling（MMM）を取り上げましたが、弊社では日々手探りの状況でMMMに取り組んでおります。Uber、FaceBook、Googleなどの企業の事例や論文から学びつつ、業務をおこなっております。今回は、その中でUberのMMM論文の紹介をしていきます！なお、MMMの詳細を知りたい方は、前のブログを見ていただければと思います。

UberのMMMの取り組み

今回紹介するのは、こちらの論文（Title:Bayesian Time Varying Coefficient Model with Applications to Marketing Mix Modeling）です。本論文のポイントとしては、UberではMMMにベイジアン時変係数モデル(BTVC：Bayesian time varying coefficient)と、経時的変化をとらえるためにカーネル回帰を使っているということです。それでは、具体的に論文の中身を紹介していきます。

背景

MMMを利用して、マーケティング効果を数値化するのには、次の6つの問題点があります。

広告技術の進化の速さが早くて、期間を長く取れない
粒度の細かいデータをとると、疎なデータしか得られなかったり外れ値が出てくる可能性がある
データの逐次性によって、誤差が時間的に相関している
内生性や多重共線性の問題もある
モデルの構築に多額の費用がかかり、利害関係者との調整コストもかかるし、解釈可能性も求められている
十分なデータがなかったりして、機械学習をするためのホールドアウトを用意できなかったする

Uberでは、これらの問題点をすべて解決することを目標にMMMの手法開発に取り組んでいます。本論文では、MMMにベイジアン時変係数モデル(BTVC)を用いた手法を用いています。

方法

マーケティング反応 $\hat y_t$ 、その回帰子 $x_{t, 1} \dots x_{t, p}$ について、次のモデルを考えます。 $g(t)$ は時系列のプロセスを示しており、 $f_{t, p}$ は費用曲線関数を示しております。

$\hat y_t = g(t) + \prod_{p=1}^{P} f_{t, p} (x_{t, p})$ ・・・（1）

式(1)からトレンドと季節を分離して、式(2)を得ます。 $exp(l_t)$ はトレンド成分、 $exp(s_t)$ は季節性の成分、 $\beta_{t, p}$ は、チャネル固有の時変係数です。

$\hat y_t = exp(l_t) exp(s_t) + \prod_{p=1}^{P} x_{t,p}^{\beta_{t, p}}$ ・・・（2）

さらに両辺対数をとって式(3)を得ます

$ln(\hat y_t) = l_t + s_t + \sum_{p=1}^{P} ln (x_{t, p}) \beta_{t, p} = l_t + s_t + r_t$ ・・・（3）

式(3)は、動的線形モデル（Dynamic Linear Model: DLM）などの状態空間モデルやカルマンフィルタで推定することが可能です。しかし、DLMのマルコフ連鎖モデルによる推定は、高次元のデータでは非効率で計算コストが高くなります。また、カルマンフィルタだと制約をかけづらく、ノイズを外れ値に強いt分布に適用しづらい問題があります。そこで、MMMのために、カーネル回帰を用いて、ベイズの枠組みで係数を時間変動させる新しいアプローチを開発したというのが本論文です。

詳細な説明については、論文を見ていただきたいのですが、1番重要なポイントは、回帰係数を局所潜在変数の加重和として表現することです。時刻 $t_j$ におけるp番目の回帰子について、潜在変数 $b_{j, p}$ を考えます。それぞれの回帰子について潜在変数の個数はJ個です。

$\beta_{t, p} = \sum_{j} w_j (t) b_{j, p}$ ・・・（4）

$w_j(t) = k(t, t_j) / \sum_{i=1}^{J} k(t, t_i)$ ・・・（5）

$k(t, t_j)$ はカーネル関数で、ガウシアン、2次関数などを使います。式(5)から、 $t_j$ とtの時間的距離を考慮して重みづけをしているのがわかります。つまり、時間が近いものほど大きい重みづけをしています。

下図は、BTVCのフローです。 $\mu_{reg}, b_{reg}$ をベイズ推定してから、 $\beta_{reg}$ を求める2段階の階層構造のモデルとなっています。推定には、確率変分推論(SVI:Stochastic Variational Inference)を使っています。詳しい説明は、論文の3.2章を見ていただければと思います。

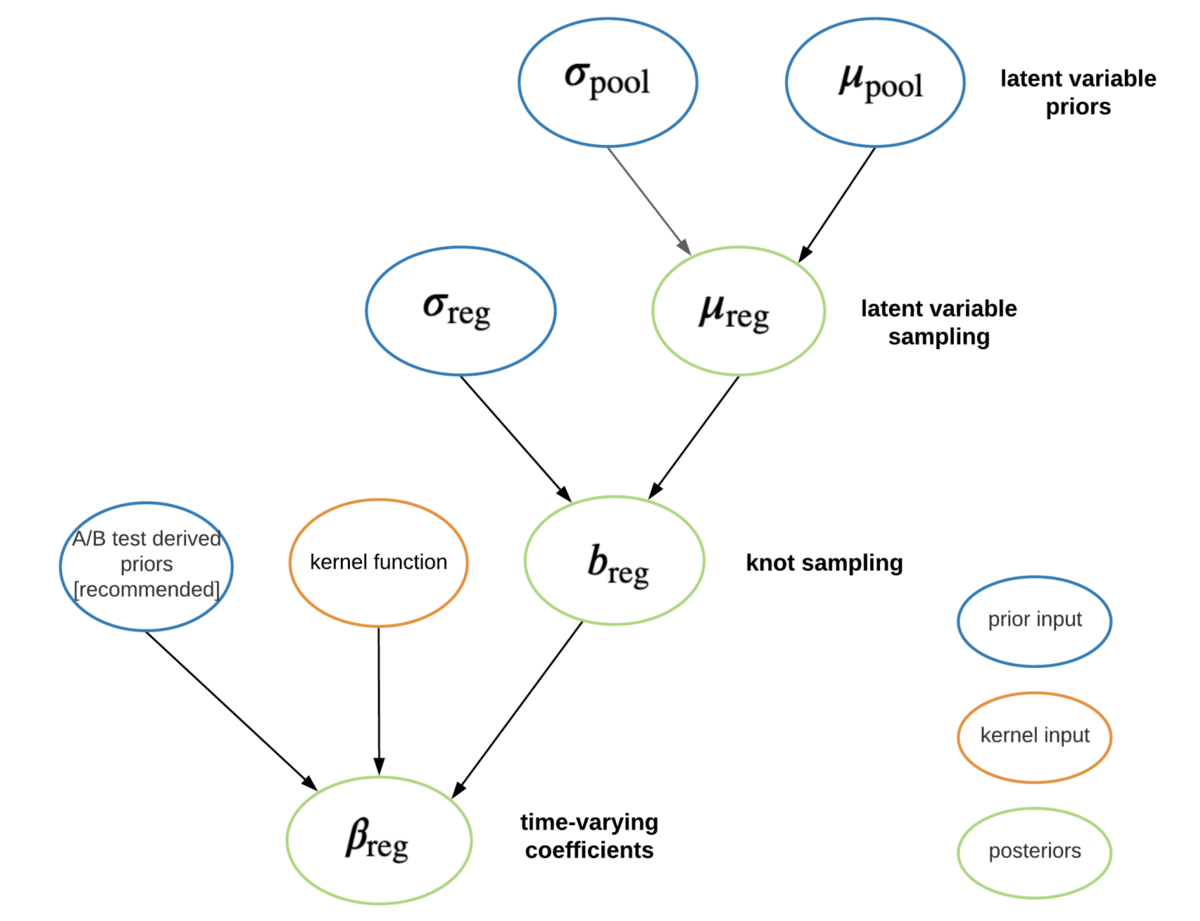（Bayesian Time Varying Coefficient Model with Applications to Marketing Mix ModelingのFigure1より引用）

結果

シミュレーションデータと実際のデータの2つで上記のモデルの精度を検証しています。

シミュレーションデータでの検証
BSTS（Bayesian structural time series）、tvREG(time varying coefficient for single and multiequation regressions)、そして今回の手法（BTVC）の、3つの手法で検証を行っています。MSE(Mean Squared Error)で誤差の評価を行った結果、Table1のような結果が得られました。いずれの手法よりもBTVCの方がMSEが小さかったという結果が得られました。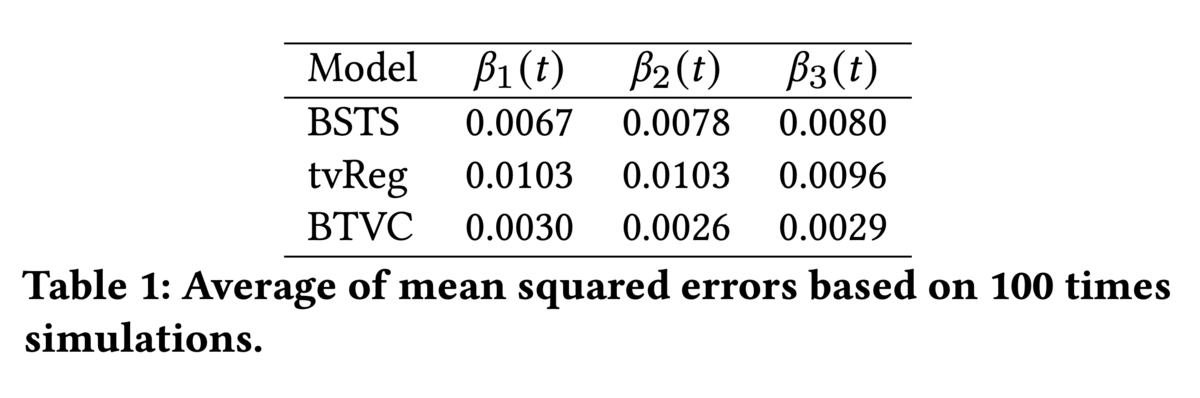（Bayesian Time Varying Coefficient Model with Applications to Marketing Mix ModelingのTable1より引用）

実際のデータでの検証
主要10ヶ国の2018年1月から2021年1月までのUberEatsのデータを使って、検証を行っています。新規に獲得したユーザーによる最初のオーダー数をSARIMA、Facebook Prophet、そして今回の手法（BTVC）の、3つの手法で検証を行っています。SMAPE(Symmetric mean absolute percentage error)でモデルの評価を行っています。

$SMAPE = \sum_{t=1}^{h} \frac{ | F_t - A_t | }{ ( | F_t | + | A_t | ) / 2}$

$F_t, A_t$ は時刻tにおける予測値と正解値を示しています。下図は、SMAPE値の平均と標準偏差を示しています。BTVCは10ヶ国の大部分において、ほかの2つのモデルを上回っている精度が出ていることがわかりました。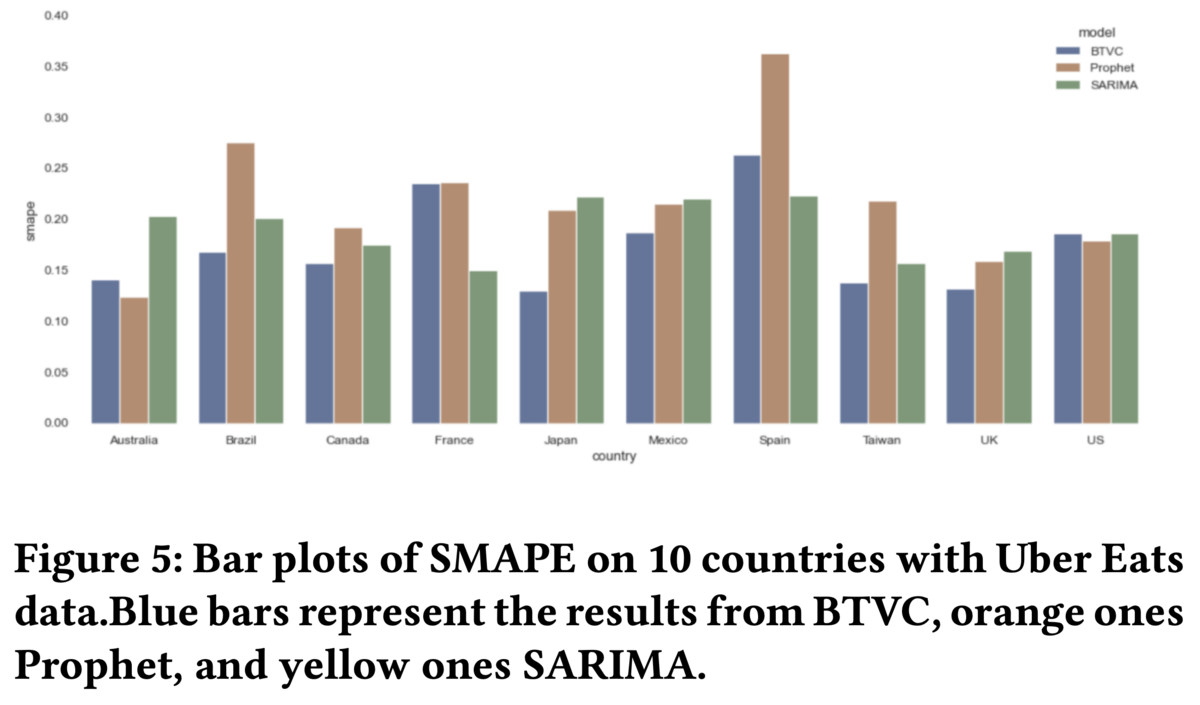（Bayesian Time Varying Coefficient Model with Applications to Marketing Mix ModelingのFigure5より引用）

論文を読んだ所感

いかがでしたでしょうか。今回は、UberのMMM論文の紹介をさせていただきました。

orbitというPythonパッケージにて著者がコードを公開してくださっているようなので、簡単に実行はできるようです。ただし本論文の手法をビジネスの現場に適用する上で、注意しなくてはいけないことが2点あると考えます。

まず、1つ目に、自社のマーケティングやプロモーションの課題を明確にし、それを改善していくためにふさわしい分析アプローチを模索していく必要があることです。マーケティング分野にはMMM以外にも、様々な調査や分析があります。いずれも目的が異なるため、予算やデータの制約に合わせて、その都度状況に合わせた調査や分析を選択していく必要があると考えます。
2つ目は、MMMは、完全には因果関係を推定出来ていないことです。因果推論をまじめにするのであれば、Judea Pearl流の因果推論アプローチをするのが順当な流れなのですが、状況によっては、コストがかかりすぎたり、不可能な場合があります。その代替案としてMMMが提案されているに過ぎないので、本質的な因果関係を意識して分析結果を眺める必要があると考えます。

今後も新しい手法を学び続けて、自社のマーケティングにデータサイエンティストとして貢献していきたいと思います。